LeetCode-W119

比较简单的一场，前3题rating竟然都没过1600

Q1 找到两个数组中的公共元素

给你两个下标从 0 开始的整数数组 nums1 和 nums2 ，它们分别含有 n 和 m 个元素。

请你计算以下两个数值：

  • 统计 0 <= i < n 中的下标 i ，满足 nums1[i] 在 nums2 中 至少 出现了一次。
  • 统计 0 <= i < m 中的下标 i ，满足 nums2[i] 在 nums1 中 至少 出现了一次。

请你返回一个长度为 2 的整数数组 answer ，按顺序 分别为以上两个数值。

示例 1：

1
2
3
4
5
输入：nums1 = [4,3,2,3,1], nums2 = [2,2,5,2,3,6]
输出：[3,4]
解释：分别计算两个数值：
- nums1 中下标为 1 ，2 和 3 的元素在 nums2 中至少出现了一次，所以第一个值为 3 。
- nums2 中下标为 0 ，1 ，3 和 4 的元素在 nums1 中至少出现了一次，所以第二个值为 4 。

示例 2：

1
2
3
输入：nums1 = [3,4,2,3], nums2 = [1,5]
输出：[0,0]
解释：两个数组中没有公共元素，所以两个值都为 0 。

提示：

  • n == nums1.length
  • m == nums2.length
  • 1 <= n, m <= 100
  • 1 <= nums1[i], nums2[i] <= 100

简单题，两个set互相遍历即可

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    fun findIntersectionValues(nums1: IntArray, nums2: IntArray): IntArray {
        val s1 = nums1.toSet()
        val s2 = nums2.toSet()
        val ret = IntArray(2)
        for (s in nums1) if (s in s2) ret[0]++
        for (s in nums2) if (s in s1) ret[1]++
        return ret
    }

}

Q2 消除相邻近似相等字符

给你一个下标从 0 开始的字符串 word 。

一次操作中，你可以选择 word 中任意一个下标 i ，将 word[i] 修改成任意一个小写英文字母。

请你返回消除 word 中所有相邻 近似相等 字符的 最少 操作次数。

两个字符 a 和 b 如果满足 a == b 或者 a 和 b 在字母表中是相邻的，那么我们称它们是 近似相等 字符。

示例 1：

1
2
3
4
输入：word = "aaaaa"
输出：2
解释：我们将 word 变为 "acaca" ，该字符串没有相邻近似相等字符。
消除 word 中所有相邻近似相等字符最少需要 2 次操作。

示例 2：

1
2
3
4
输入：word = "abddez"
输出：2
解释：我们将 word 变为 "ybdoez" ，该字符串没有相邻近似相等字符。
消除 word 中所有相邻近似相等字符最少需要 2 次操作。

示例 3：

1
2
3
4
输入：word = "zyxyxyz"
输出：3
解释：我们将 word 变为 "zaxaxaz" ，该字符串没有相邻近似相等字符。
消除 word 中所有相邻近似相等字符最少需要 3 次操作

提示：

  • 1 <= word.length <= 100
  • word 只包含小写英文字母。

贪心，思维题。从左往右遍历，当遇到下标i和 i + 1的字母不符合条件时贪心的将i + 1的修改，因为i + 1和i + 2可能也不符合，我们无需考虑修改成什么字符，一定可以修改成既满足i和i + 1又满足i + 1和i + 2。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import kotlin.math.abs

class Solution {
    fun removeAlmostEqualCharacters(word: String): Int {
        val chars = word.toCharArray()
        val len = word.length
        var ans = 0
        var i = 0
        while (i < len - 1) {
            if (check(chars[i], chars[i + 1])) {
                i += 2
                ans++
            } else {
                i++
            }
        }
        return ans
    }

    fun check(c1: Char, c2: Char): Boolean {
        val i = c1 - c2
        return abs(i) <= 1
    }
}

Q3 最多 K 个重复元素的最长子数组

给你一个整数数组 nums 和一个整数 k 。

一个元素 x 在数组中的 频率 指的是它在数组中的出现次数。

如果一个数组中所有元素的频率都 小于等于 k ，那么我们称这个数组是 好 数组。

请你返回 nums 中 最长好 子数组的长度。

子数组 指的是一个数组中一段连续非空的元素序列。

示例 1：

1
2
3
4
输入：nums = [1,2,3,1,2,3,1,2], k = 2
输出：6
解释：最长好子数组是 [1,2,3,1,2,3] ，值 1 ，2 和 3 在子数组中的频率都没有超过 k = 2 。[2,3,1,2,3,1] 和 [3,1,2,3,1,2] 也是好子数组。
最长好子数组的长度为 6 。

示例 2：

1
2
3
4
输入：nums = [1,2,1,2,1,2,1,2], k = 1
输出：2
解释：最长好子数组是 [1,2] ，值 1 和 2 在子数组中的频率都没有超过 k = 1 。[2,1] 也是好子数组。
最长好子数组的长度为 2 。

示例 3：

1
2
3
4
输入：nums = [5,5,5,5,5,5,5], k = 4
输出：4
解释：最长好子数组是 [5,5,5,5] ，值 5 在子数组中的频率没有超过 k = 4 。
最长好子数组的长度为 4 。

提示：

  • 1 <= nums.length <= 105
  • 1 <= nums[i] <= 109
  • 1 <= k <= nums.length

这种滑动窗口上LC上太多了，所以本题作为Q3连1600都不到的原因。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    fun maxSubarrayLength(nums: IntArray, k: Int): Int {
        var ans = 0
        val n = nums.size
        val mp = hashMapOf<Int, Int>()
        var l = 0
        for (r in 0..<n) {
            mp[nums[r]] = mp.getOrDefault(nums[r], 0) + 1
            while (mp[nums[r]]!! > k) {
                mp[nums[l]] = mp[nums[l]]!! - 1
                l++
            }
            ans = maxOf(ans, r - l + 1)
        }
        return ans
    }
}

Q4 关闭分部的可行集合数目

一个公司在全国有 n 个分部，它们之间有的有道路连接。一开始，所有分部通过这些道路两两之间互相可以到达。

公司意识到在分部之间旅行花费了太多时间，所以它们决定关闭一些分部（也可能不关闭任何分部），同时保证剩下的分部之间两两互相可以到达且最远距离不超过 maxDistance 。

两个分部之间的 距离 是通过道路长度之和的 最小值 。

给你整数 n ，maxDistance 和下标从 0 开始的二维整数数组 roads ，其中 roads[i] = [ui, vi, wi] 表示一条从 ui 到 vi 长度为 wi的 无向 道路。

请你返回关闭分部的可行方案数目，满足每个方案里剩余分部之间的最远距离不超过 maxDistance。

注意，关闭一个分部后，与之相连的所有道路不可通行。

注意，两个分部之间可能会有多条道路。

示例 1：

img

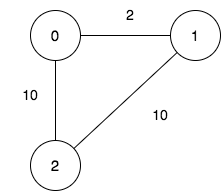
1
2
3
4
5
6
7
8
9
输入：n = 3, maxDistance = 5, roads = [[0,1,2],[1,2,10],[0,2,10]]
输出：5
解释：可行的关闭分部方案有：
- 关闭分部集合 [2] ，剩余分部为 [0,1] ，它们之间的距离为 2 。
- 关闭分部集合 [0,1] ，剩余分部为 [2] 。
- 关闭分部集合 [1,2] ，剩余分部为 [0] 。
- 关闭分部集合 [0,2] ，剩余分部为 [1] 。
- 关闭分部集合 [0,1,2] ，关闭后没有剩余分部。
总共有 5 种可行的关闭方案。

示例 2：

img

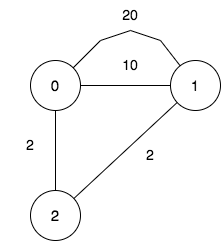
1
2
3
4
5
6
7
8
9
10
11
输入：n = 3, maxDistance = 5, roads = [[0,1,20],[0,1,10],[1,2,2],[0,2,2]]
输出：7
解释：可行的关闭分部方案有：
- 关闭分部集合 [] ，剩余分部为 [0,1,2] ，它们之间的最远距离为 4 。
- 关闭分部集合 [0] ，剩余分部为 [1,2] ，它们之间的距离为 2 。
- 关闭分部集合 [1] ，剩余分部为 [0,2] ，它们之间的距离为 2 。
- 关闭分部集合 [0,1] ，剩余分部为 [2] 。
- 关闭分部集合 [1,2] ，剩余分部为 [0] 。
- 关闭分部集合 [0,2] ，剩余分部为 [1] 。
- 关闭分部集合 [0,1,2] ，关闭后没有剩余分部。
总共有 7 种可行的关闭方案。

示例 3：

1
2
3
4
5
6
输入：n = 1, maxDistance = 10, roads = []
输出：2
解释：可行的关闭分部方案有：
- 关闭分部集合 [] ，剩余分部为 [0] 。
- 关闭分部集合 [0] ，关闭后没有剩余分部。
总共有 2 种可行的关闭方案。

提示：

  • 1 <= n <= 10
  • 1 <= maxDistance <= 105
  • 0 <= roads.length <= 1000
  • roads[i].length == 3
  • 0 <= ui, vi <= n - 1
  • ui != vi
  • 1 <= wi <= 1000
  • 一开始所有分部之间通过道路互相可以到达。

本场的困难题,rating 2077,算是一道比较简单的困难题了，首先观察数据范围n小于10,那么第一想到求最短路的就是floyd,暴力枚举所有方案也才最多1024种，那么就可以完全暴力枚举了，判断连通的话，通常做法为并查集，但这里都用floyd了，计算途中就可以判断联通了，反正n最大也才10,随便都可以啦。代码有点屎。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Solution {
    public int numberOfSets(int n, int maxDistance, int[][] roads) {
        int ans = 0;
        for (int i = 0; i < 1 << n; i++) {
            if (check(i, maxDistance, roads, n)) ans++;
        }
        return ans;
    }

    private boolean check(int i, int maxDistance, int[][] roads, int n) {
        if (i == 0) return true;
        int[] p = new int[n];
        for (int j = 0; j < n; j++) {
            p[j] = j;
        }
        int[][] g = new int[n][n];
        for (var gg : g) Arrays.fill(gg, 0x3f3f3f3f);
        for (var road : roads) {
            int a = road[0], b = road[1], d = road[2];
            if ((i & 1 << a) == 0 || (i & 1 << b) == 0) continue;
            g[a][b] = g[b][a] = Math.min(g[a][b], d);
            int pa = find(p, a), pb = find(p, b);
            if (pa != pb) p[pa] = pb;
        }
        Set<Integer> set = new HashSet<>();
        for (int j = 0; j < n; j++) {
            if ((i & 1 << j) != 0) set.add(find(p, j));
        }
        if (set.size() > 1) return false;
        int maxD = -0x3f3f3f3f;
        for (int k = 0; k < n; k++) {
            for (int j = 0; j < n; j++) {
                for (int l = 0; l < n; l++) {
                    if ((i >> k & 1) == 1 && (i >> j & 1) == 1 && (i >> l & 1) == 1) {
                        g[j][l] = Math.min(g[j][l], g[j][k] + g[k][l]);
                    }
                }
            }
        }
        for (int j = 0; j < n; j++) {
            for (int k = j + 1; k < n; k++) {
                if ((i >> j & 1) == 1 && (i >> k & 1) == 1)
                    maxD = Math.max(maxD, g[j][k]);
            }
        }
        return maxD <= maxDistance;
    }


    int find(int[] p, int a) {
        if (a == p[a]) return a;
        return p[a] = find(p, p[a]);
    }

}
算法
#leetcode
LeetCode-W119
http://example.com/2023/12/31/LeetCode-W119/
作者
ykexc
发布于
2023年12月31日
许可协议