差分&二分
给你一个下标从 0 开始的二维整数数组 flowers ,其中 flowers[i] = [starti, endi] 表示第 i 朵花的 花期 从 starti 到 endi (都 包含)。同时给你一个下标从 0 开始大小为 n 的整数数组 people ,people[i] 是第 i 个人来看花的时间。
请你返回一个大小为 n 的整数数组 answer ,其中 answer[i]是第 i 个人到达时在花期内花的 数目 。
示例 1:
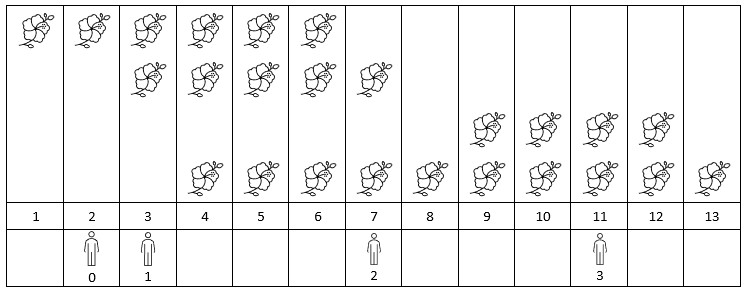
1 | |
示例 2:
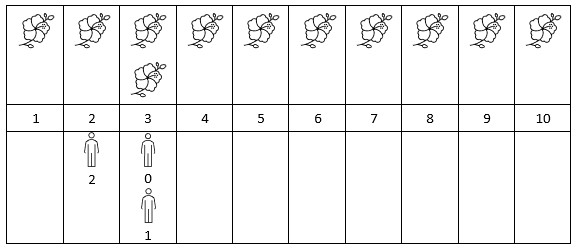
1 | |
提示:
1 <= flowers.length <= 5 * 104flowers[i].length == 21 <= starti <= endi <= 1091 <= people.length <= 5 * 1041 <= people[i] <= 109
对于此题首先想到的就是离散化+差分,但后来想了想二分也很适合解决此类问题
-
差分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public int[] fullBloomFlowers(int[][] flowers, int[] people) {
Set<Integer> set = new TreeSet<>();
for (var flower : flowers) {
set.add(flower[0]);
set.add(flower[1]);
}
for (var e : people) set.add(e);
int p = 1;
Map<Integer, Integer> map = new HashMap<>();
for (var s : set) map.put(s, p++);
int[] diff = new int[p + 1];
for (var flower : flowers) {
diff[map.get(flower[0])]++;
diff[map.get(flower[1]) + 1]--;
}
for (int i = 1; i <= p; i++) {
diff[i] += diff[i - 1];
}
int[] ans = new int[people.length];
for (int i = 0; i < people.length; i++) {
ans[i] = diff[map.get(people[i])];
}
return ans;
}
} -
二分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public int[] fullBloomFlowers(int[][] flowers, int[] people) {
int n = flowers.length;
int[] start = new int[n];
int[] end = new int[n];
IntStream.range(0, n).forEach(idx -> {
start[idx] = flowers[idx][0];
end[idx] = flowers[idx][1];
});
Arrays.sort(start);
Arrays.sort(end);
return Arrays.stream(people).map(person -> binarySearch(start, person) - binarySearch(end, person - 1)).toArray();
}
int binarySearch(int[] arr, int v) {
int l = 0, r = arr.length - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (arr[mid] <= v) l = mid;
else r = mid - 1;
}
return arr[l] <= v ? l : -1;
}
}
对于二维情况下两种思路同样适用
给你一个二维整数数组 rectangles ,其中 rectangles[i] = [li, hi] 表示第 i 个矩形长为 li 高为 hi 。给你一个二维整数数组 points ,其中 points[j] = [xj, yj] 是坐标为 (xj, yj) 的一个点。
第 i 个矩形的 左下角 在 (0, 0) 处,右上角 在 (li, hi) 。
请你返回一个整数数组 count ,长度为 points.length,其中 count[j]是 包含 第 j 个点的矩形数目。
如果 0 <= xj <= li 且 0 <= yj <= hi ,那么我们说第 i 个矩形包含第 j 个点。如果一个点刚好在矩形的 边上 ,这个点也被视为被矩形包含。
示例 1:
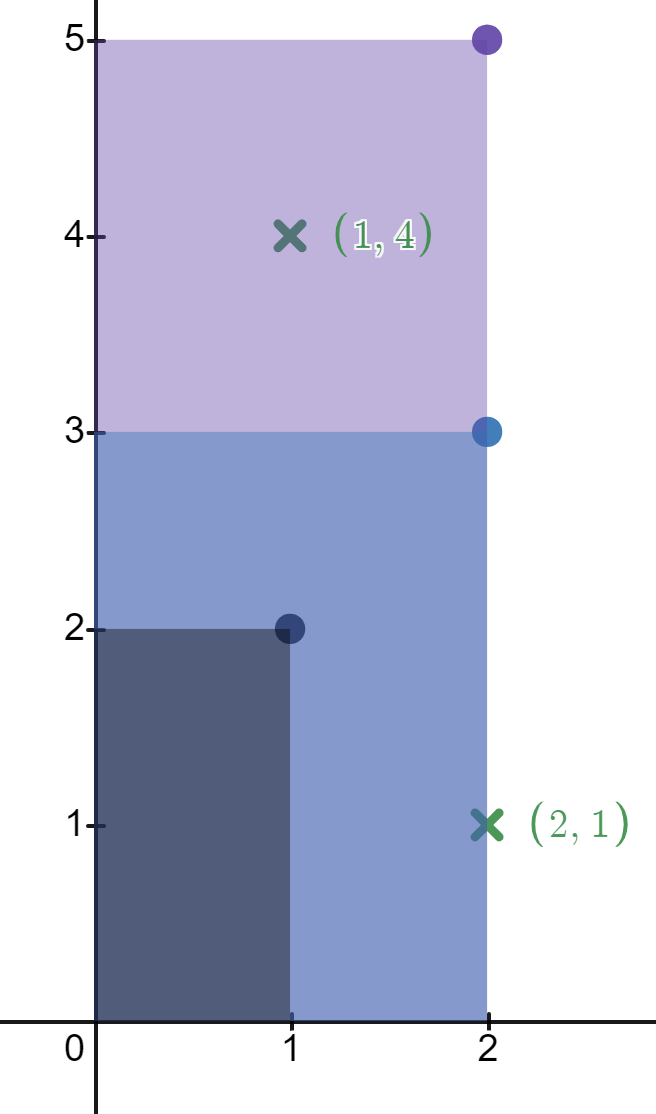
1 | |
示例 2:
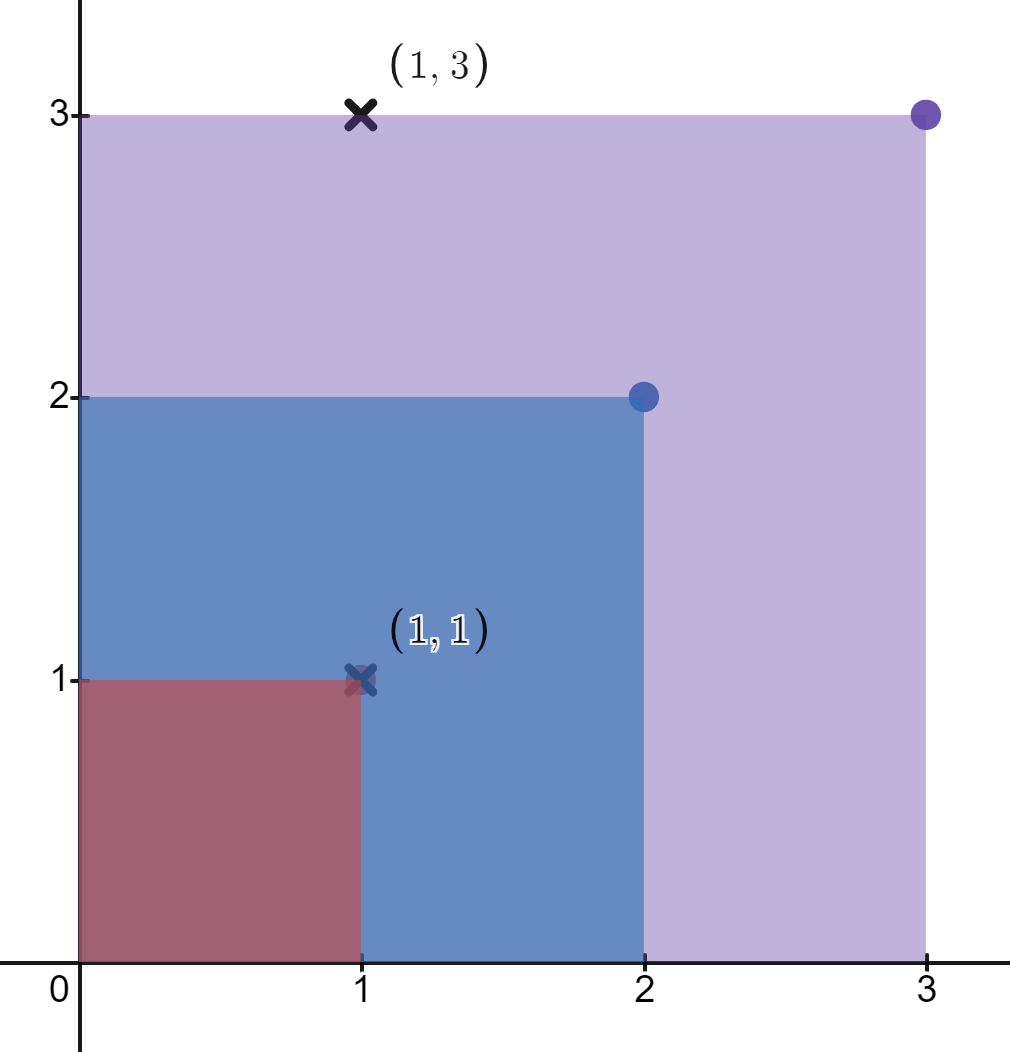
1 | |
提示:
-
1 <= rectangles.length, points.length <= 5 * 104 -
rectangles[i].length == points[j].length == 2 -
1 <= li, xj <= 109 -
1 <= hi, yj <= 100 -
所有
rectangles互不相同 。 -
所有
points互不相同 。 -
差分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41class Solution {
public int[] countRectangles(int[][] rectangles, int[][] points) {
Set<Integer> set = new TreeSet<>();
int g = -1;
set.add(0);
for (var rectangle : rectangles) {
set.add(rectangle[0]);
set.add(rectangle[1]);
g = Math.max(g, rectangle[1]);
}
for (var point : points) {
set.add(point[0]);
set.add(point[1]);
g = Math.max(g, point[1]);
}
Map<Integer, Integer> map = new HashMap<>();
int p = 1;
for (var e : set) map.put(e, p++);
int m = map.get(g);
int[][] diff = new int[p + 1][m + 2];
for (var rectangle : rectangles) {
int x = map.get(rectangle[0]), y = map.get(rectangle[1]);
diff[1][1]++;
diff[1][y + 1]--;
diff[x + 1][1]--;
diff[x + 1][y + 1]++;
}
for (int i = 1; i <= p; i++) {
for (int j = 1; j <= m; j++) {
diff[i][j] += diff[i - 1][j] + diff[i][j - 1] - diff[i - 1][j - 1];
}
}
int n = points.length;
int[] ans = new int[n];
for (int i = 0; i < n; i++) {
int x = map.get(points[i][0]), y = map.get(points[i][1]);
ans[i] = diff[x][y];
}
return ans;
}
} -
二分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37class Solution {
int[][] _rectangles;
public int[] countRectangles(int[][] rectangles, int[][] points) {
this._rectangles = rectangles;
Arrays.sort(_rectangles, Comparator.comparing(e -> e[0]));
int n = rectangles.length, m = points.length;
int[][] sum = new int[n][101];
sum[n - 1][_rectangles[n - 1][1]] = 1;
for (int i = n - 2; i >= 0; i--) {
System.arraycopy(sum[i + 1], 0, sum[i], 0, 101);
sum[i][_rectangles[i][1]] += 1;
}
for (int i = 0; i < n; i++) {
for (int j = 99; j >= 0; j--) {
sum[i][j] += sum[i][j + 1];
}
}
int[] ans = new int[m];
for (int i = 0; i < m; i++) {
int x = points[i][0], y = points[i][1];
int k = binarySearch(x);
if (k != -1) ans[i] = sum[k][y];
}
return ans;
}
int binarySearch(int x) {
int l = 0, r = _rectangles.length - 1;
while (l < r) {
int mid = l + r >> 1;
if (_rectangles[mid][0] >= x) r = mid;
else l = mid + 1;
}
return _rectangles[l][0] >= x ? l : -1;
}
}